概念

如果一个 Node 中只有一个指针域，则被称为单链表。

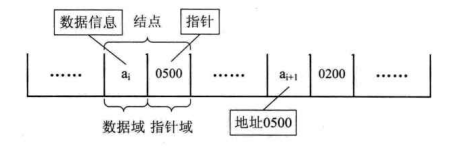
优点：

• 插入和删除高效，时间复杂度为 O(1)。
• 不需要提前分配存储空间，元素个数不受限制。

缺点：

• 查询较慢，时间复杂度为 O(n)。

单链表实现

抽象数据类型

class Node {
    // 数据域
    public Object data;
    // 指针域
    public Node next;

    public Node() {}

    public Node(Object obj) {
        data = obj;
    }

    @Override
    public String toString() {
        return data.toString();
    }
}

public class LinkList {
    private Node head;
    private int size;

    public LinkList() {
        head = new Node();
    }
}

插入结点

假设要在结点 p 和 p->next 结点之间插入结点 s，则需要两步：

1. 让 s->next = p->next;
2. 让 p->next = s。

注意：先后顺序不可调。

插入前：

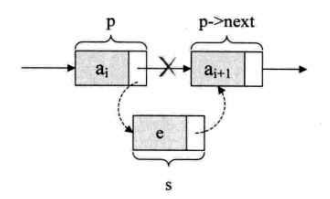
插入后：

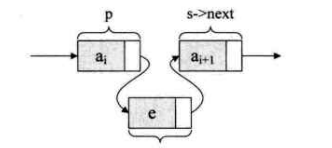
思路：

1. 声明一个结点 p 指向链表头结点，初始化 j 从 0 开始；
2. 当 j < i 时，就遍历链表，让 p 的指针向后移动，不断指向下一个结点，j 累加 1；
3. 在系统中生成一个空结点 s；
4. 将数据元素 e 赋值给 s-> data;
5. 然后执行 s->next = p->next、p->next = s；
6. 链表长度+1；
7. 返回成功。

    /**
     * 在指定位置插入新结点
     *
     * @param obj
     * @param i
     */
    public boolean insert(Object obj, int i) {
        if (i < 0 || i > size) {
            System.out.println("插入位置不正确");
            return false;
        }

        Node s = new Node(obj);
        Node p = head;

        for (int j = 0; j < i; j++) {
            p = p.next;
        }

        s.next = p.next;
        p.next = s;

        size++;
        return true;
    }

删除结点

删除的主要逻辑是让 p->next = p->next->next，如果要返回删除的元素（p->next），则需要现将 p->next 保存在临时变量中，然后执行删除逻辑，即 t -> p->next，p->next = p->next->next。

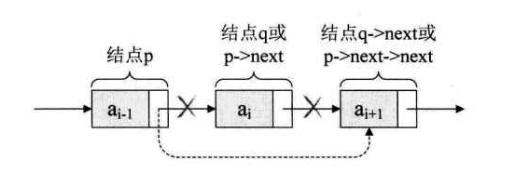
思路：

1. 声明一个节点 p 指向链表头结点，初始化 j 从 0 开始；
2. 当 j< i 时，就遍历链表，让 p 的指针向后移动，不断指向下一个结点，j 累加 1；
3. 若到链表末尾 p->next 为空，则说明第 i 个元素不存在；
4. 否则查找成功，将欲删除的结点 p-> next 赋给 t；
5. 执行 p->next = p->next->next；
6. 将 t 结点的数据 t->data 返回；
7. 链表长度-1；
8. 返回。

    /**
     * 删除指定位置的元素
     *
     * @param i
     * @return
     */
    public Node remove(int i) {
        if (i < 0 || i > size - 1) {
            System.out.println("删除位置不正确");
            return null;
        }

        Node p = head;
        for (int j = 0; j < i; j++) {
            p = p.next;
        }

        if (p.next == null) {
            // 没找到
            return null;
        } else {
            // 找到了
            Node t = p.next;
            p.next = p.next.next;
            size--;
            return t;
        }
    }

查找结点

查找第 i 个元素：

1. 申明一个结点 p 指向链表头结点，初始化 j 从 0 开始；
2. 当 j< i 时，让 p 的指针向后移动，不断指向向下一个结点，j 累加 1；
3. 若到链表末尾 p 为空，则说明第 i 个元素不存在；
4. 否则查找成功，返回结点 p 的数据。

    /**
     * 查找第i个元素
     *
     * @param i
     * @return
     */
    public Object search(int i) {
        Node p = head;

        // i 有可能为0
        for (int j = 0; j <= i; j++) {
            p = p.next;
        }

        if (p == null) {
            return -1;
        } else {
            return p.data;
        }
    }

完整代码

package com.sqlboy.lineartable;

public class LinkList {
    private Node head;
    private int size;

    public LinkList() {
        head = new Node();
    }

    /**
     * 创建空链表，只有头结点
     */
    public void createList() {
        head.next = null;
        size = 0;
    }

    /**
     * 整表创建空链表
     *
     * @param n
     */
    public void createList(int n) {
        // 创建一个Node，表示前置结点
        Node preNode = null;

        for (int i = 0; i < n; i++) {
            // 创建一个当前节点
            Node node = new Node();

            if (i == 0) {
                head.next = node;
            } else {
                preNode.next = node;
            }

            preNode = node;
            size++;
        }
    }

    /**
     * 打印链表
     */
    public void show() {
        Node node = head.next;
        for (int i = 0; i < size; i++) {
            System.out.println(node.data);
            node = node.next;
        }
        System.out.println();
    }

    /**
     * 在指定位置插入新结点
     *
     * @param obj
     * @param i
     */
    public boolean insert(Object obj, int i) {
        if (i < 0 || i > size) {
            System.out.println("插入位置不正确");
            return false;
        }

        Node s = new Node(obj);
        Node p = head;

        for (int j = 0; j < i; j++) {
            p = p.next;
        }

        s.next = p.next;
        p.next = s;

        size++;
        return true;
    }

    /**
     * 查找第i个元素
     *
     * @param i
     * @return
     */
    public Object search(int i) {
        Node p = head;

        // i 有可能为0
        for (int j = 0; j <= i; j++) {
            p = p.next;
        }

        if (p == null) {
            return -1;
        } else {
            return p.data;
        }
    }

    /**
     * 删除指定位置的元素
     *
     * @param i
     * @return
     */
    public Node remove(int i) {
        if (i < 0 || i > size - 1) {
            System.out.println("删除位置不正确");
            return null;
        }

        Node p = head;
        for (int j = 0; j < i; j++) {
            p = p.next;
        }

        if (p.next == null) {
            // 没找到
            return null;
        } else {
            // 找到了
            Node t = p.next;
            p.next = p.next.next;
            size--;
            return t;
        }
    }

    public static void main(String[] args) {
        LinkList list = new LinkList();
        list.insert(new Integer(0), 0);
        list.insert(new Integer(1), 1);
        list.insert(new Integer(2), 2);
        list.insert(new Integer(3), 3);

        list.show();

        System.out.println(list.remove(3));
        System.out.println();
        list.show();


//        LinkList list2 = new LinkList();
//        list2.createList(5);
//        list2.show();
    }
}

class Node {
    // 数据域
    public Object data;
    // 指针域
    public Node next;

    public Node() {}

    public Node(Object obj) {
        data = obj;
    }

    @Override
    public String toString() {
        return data.toString();
    }
}