数据结构与算法

数据结构与算法概述

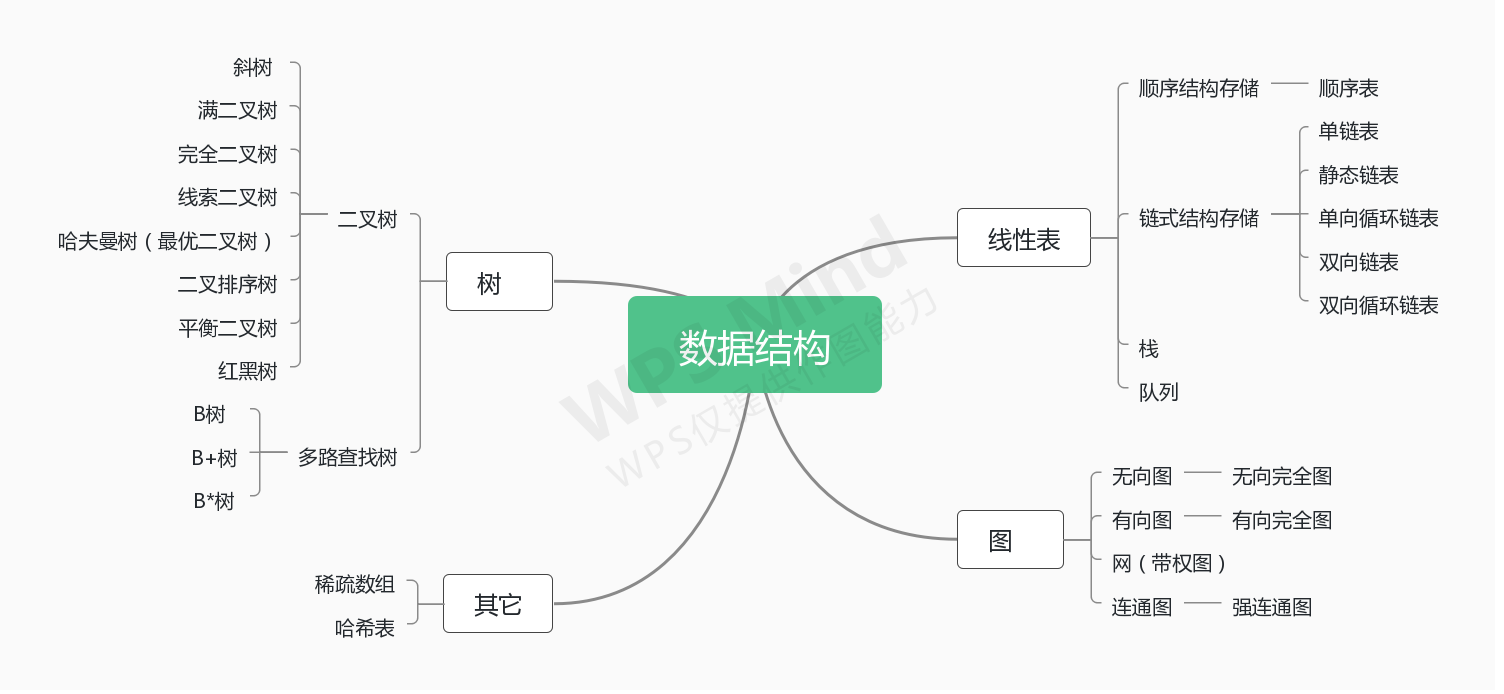
# 数据结构

数据结构是相关之间存在一种或多种特定关系的数据元素的集合，数据结构分为线性结构和非线性结构。

# 线性结构

线性结构也称线性表，指的是零个或多个数据元素的有限序列。常见的线性表：

数组
链表
队列
栈

# 非线性结构

非线性结构和线性结构对立，存储元素之间不存在一对一的线性关系。

常见的非线性结构有：

多维数组
广义表
树
图

# 算法

算法是解决特定问题求解步骤的描述，在计算机中表现为指令的有限序列，并且每条指令都表示一个或多个操作。

# 时间复杂度

算法效率的度量方法：

事后统计法。这种方法主要是通过设计好的测试程序和数据，利用计算机计时器对不同算法编制的程序的运行时间进行比较，从而确定算法效率的高低。
事前分析估算法。在计算机程序编制前，依据统计方法对算法进行估算，如根据时间复杂度来估算算法时间效率。

一般情况下，算法中的基本操作语句的重复执行次数是问题规模 n 的某个函数，用 T(n)表示。若有某个辅助函数 f(n)，使得当 n 接近于无穷大时，T(n) / f(n)的极限值为不等于零的常数，则称 f(n)是 T(n)的同数量级函数。记作 T(n) = O(f(n))。它表示岁问题规模 n 的增大，算法执行时间的增长率和 f(n)的增长率相同，称作算法的渐进时间复杂度，简称为时间复杂度。这样用大 O()来体现算法时间复杂度的方法，我们称之为大 O 记法。

如何计算时间复杂度？

用常数 1 取代运行事件中的所有加法常数。T(n) = 3n^3 + 2n^2 + 8 推导出 T(n) = 3n^3 + 2n^2 + 1。
在修改后的运行次数函数中，只保留最高阶项。T(n) = 3n^3 + 2n^2 + 1 推导出 T(n) = 3n^3。
如果最高阶项存在且不是 1，则去除与这个项目相乘的常数，得到的结果就是大 O 阶。T(n) = 3n^3 推导出 T(n) = n^3，即 O(n^3)。

常见的时间复杂度：

常数阶 O(1)
对数阶 O(log2n)
线性阶 O(n)
线性对数阶 O(nlog2n)
平方阶 O(n^2)
立方阶 O(n^3)
K 次方阶 O(n^k)
指数阶 O(2^n)

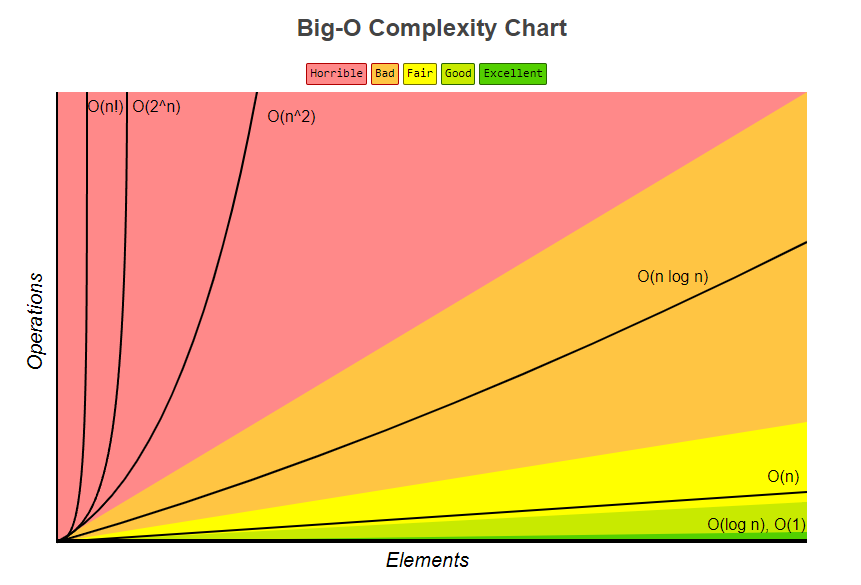
从上往下，时间复杂度依次增大，且随着问题规模 n 的增大，差异愈发明显。常见算法时间复杂度代码示例如下：

常数阶：

int a = 0;
int b = 0;
int c = a + b;

1
2
3

对数阶：

int count = 1;

while(count < n) {
    count = count * 2
}

1
2
3
4
5

线性阶：

for (int i = 0; i < n; i++){
    // 时间复杂度为O(1)的算法
}

1
2
3

线性对数阶：

for (int j = 0; j < n; j++){
    int i = n;

    while(i < n){
        // 时间复杂度为O(1)的算法
    }
}

1
2
3
4
5
6
7

平方阶：

for (int i = 0; i < n; i++){
    for (int j = 0; j < n; j++){
        // 时间复杂度为O(1)的算法
    }
}

1
2
3
4
5

最坏时间复杂度 & 平均时间复杂度：

最坏时间复杂度是指的是在最坏情况下的时间复杂度，可以保证算法在任何输入情况下都不会比最坏时间复杂度更糟糕。我们通常所说的时间复杂度都是最坏时间复杂度。平均时间复杂度就是从概率的角度，计算所有输入情况下的平均时间。

# 空间复杂度

算法的空间复杂度通过计算算法所需的存储空间实现的。和时间复杂度类似，记作：S(n) = O(f(n))，其中 n 为问题的规模，f(n)为关于 n 所占存储空间的函数。

时间复杂度指的是对运行时间的需求，空间复杂度指的是对运行空间的需求。在实际工作中通常会使用空间换时间的做法，所以我们一般讨论的复杂度都是时间复杂度。

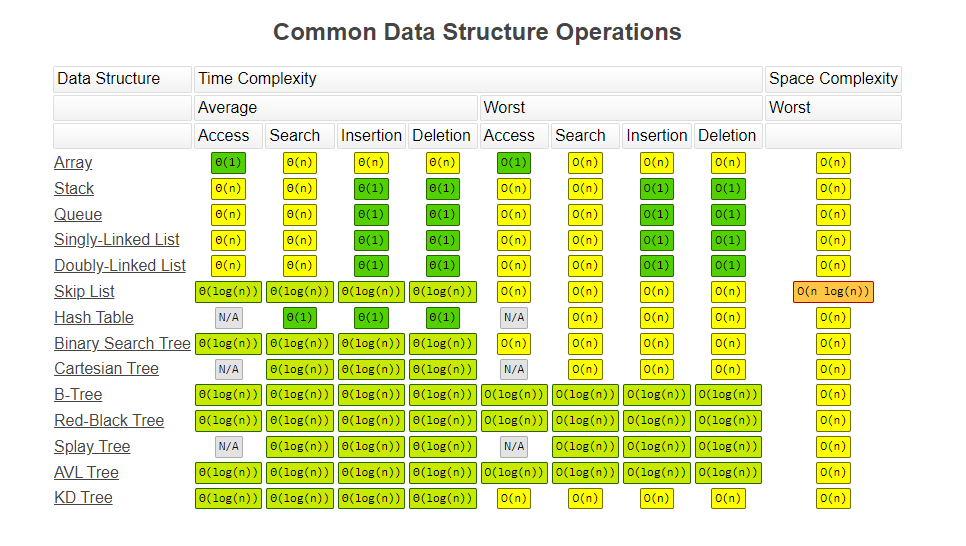
常用数据结构操作复杂度：

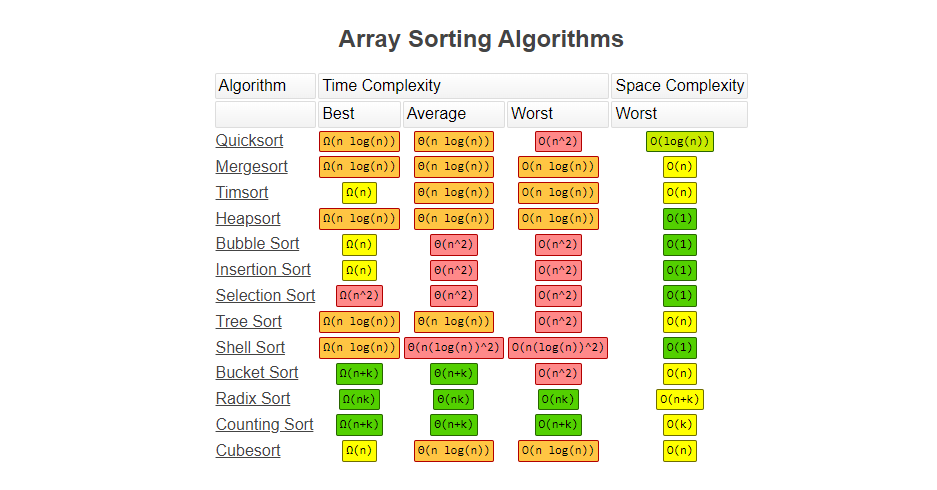
数组排序复杂度：

# 算法可视化网站

# 参考资料

《大话数据结构》
《数据结构与算法分析》
《算法导论》

上次更新: 2023/11/01, 03:11:44

线性表 - 基础概念→