图 - 存储方式
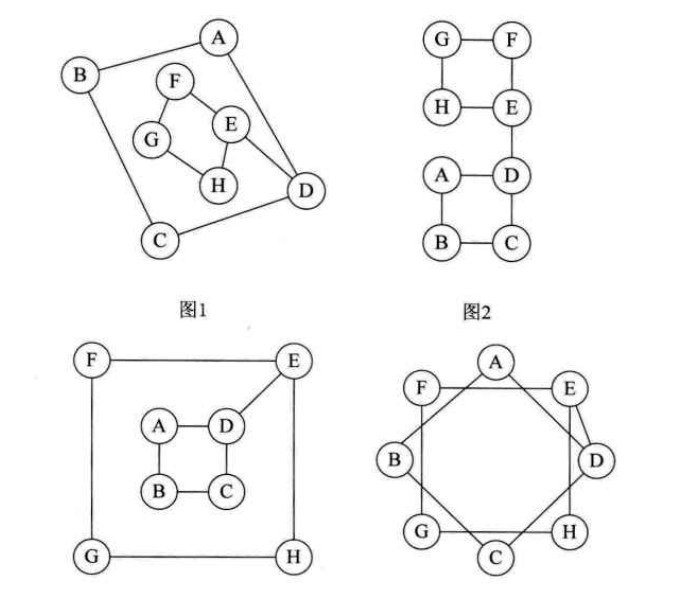
图的存储结果相对于线性表和树来讲是比较复杂的,因为图中的顶点不像线性表中的元素或树中的结点一样有先后顺序。从图的逻辑结构来看,任意一个顶点都可以看成是第一个顶点,而且逻辑结构相同的图可以以同的物理方式呈现。如下图中的四个图其实是同一个逻辑结构(同一个图)。
相对于线性表和树而已,图的物理存储是比较麻烦的,目前有五种存储结构。
- 邻接矩阵
- 邻接表
- 十字链表
- 邻接多重表
- 边集数组
# 邻接矩阵
图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图的顶点信息,一个二维数组(邻接矩阵)存储图中的边或弧的信息。
# 无向图表示
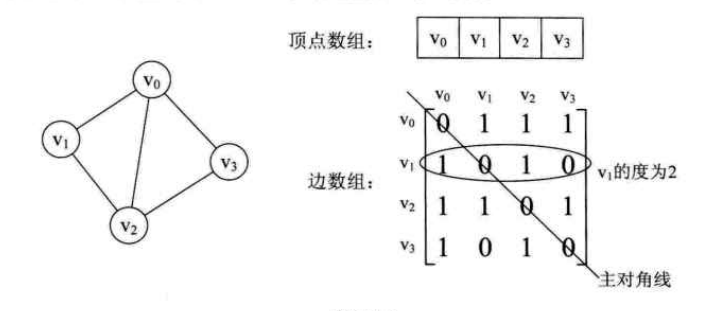
如上图所示的无向图,顶点数组为 vertex[4]={v0,v1,v2,v3},边数组 arc[4][4] 为右侧中的矩阵。由于不存在顶点到自身的边,所以对角线上的数值全为 0。由于是无向图,所以只要存在 v0 到 v1 的边,则一定存在 v1 到 v0 的边;类似地,如果存在 v1 到 v2 的边,也一定存在 v2 到 v1 的边,所以右侧的边数组是一个对称矩阵。arc[0][1]=1 表示存在 v0 到 v1 的边,arc[1][3]=0 表示不存在 v1 到 v3 的边。
基于邻接矩阵表示法,可以很便利地了解无向图的一些信息:
- 要判断 vi 和 vj 之间是否有边只需要确定 arc[i][j] 是否等于 1。
- 要知道顶点 vi 的度,只需要知道邻接矩阵中第 i 行的元素之和,如 v1 的度为 1+0+1+0=2。
- 顶点 vi 的所有邻接点就是邻接矩阵中第 i 行中值为 1 对应的点。
# 有向图表示
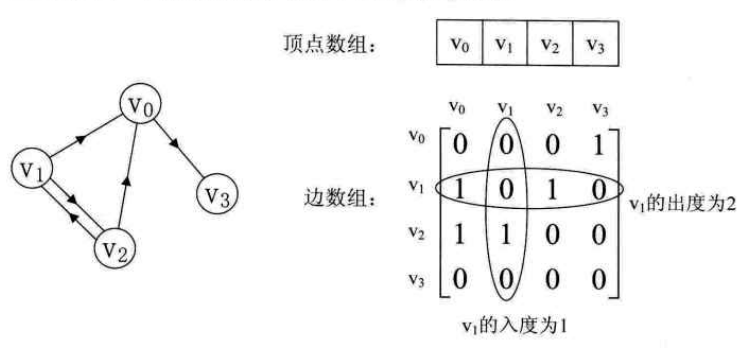
如上所示的有向图,顶点数组为 vertex[4]={v0,v1,v2,v3},弧数组 arc[4][4] 为右侧的矩阵。由于不存在顶点到自身的边,所有对角线上的数值全为 0。但由于是有向图,所以并不是对称矩阵。
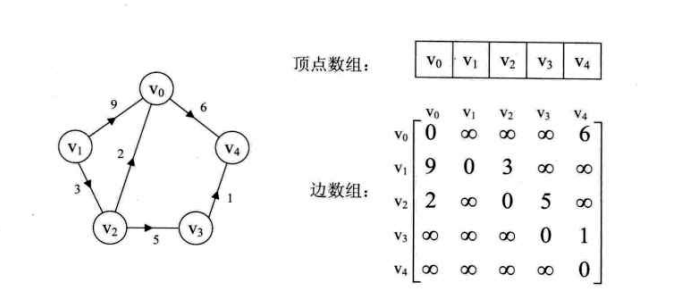
# 带权图表示
对于带权的图,如果用邻接矩阵表示,就需要将矩阵中对应位置的数值替换成权值,而不是 1,如下图所示:
# 邻接表
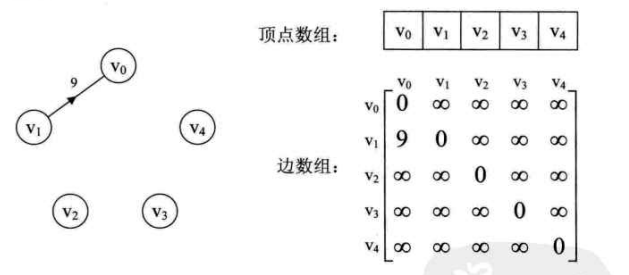
邻接矩阵是一种不错的图存储结构,但是对于稀疏图(边比较少)使用邻接矩阵会造成很大的空间浪费。如下图所示,邻接矩阵中除了 arc[1][0] 有值,其余空间都是没有使用的。
在线性表中为了避免顺序存储的空间浪费,于是采用了链式存储。邻接表就是一种将数组与链表结合的存储方式。邻接表的处理方式如下:
- 图中顶点用一个一维数组存储(也可以用链表,但是数组读取顶点更方便),数组中除了存储顶点的信息外,还要额外存储执行第一个邻接点的指针,以便于查找该顶点的边信息。
- 图中每个顶点 vi 的所有邻接点构成一个线性表,由于邻接点的个数不定,所以采用单链表存储,无向图称为顶点 vi 的边表,有向图称为顶点 vi 弧尾的出边表。
# 无向图表示
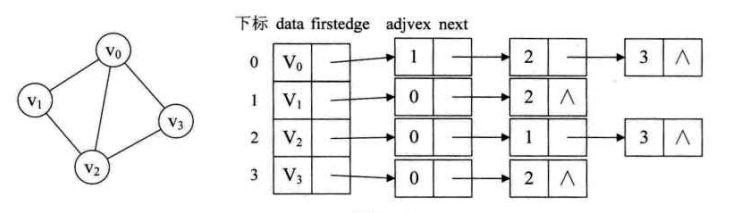
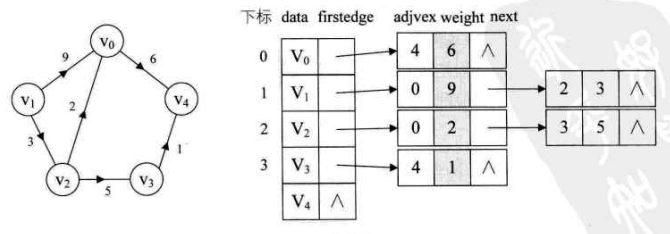
如上图所示,每个顶点包含两部分信息,data 是数据域,存储顶点的信息,firstedge 是指针域,指向边表的第一个结点。边表中每个结点包含 adjvex 和 next 两个域,adjvex 是邻接点域,存储某顶点的邻接点在顶点表中的下标,next 则存储指向边表中下一个结点的指针。
基于邻接表的表示法,可以很便利地了解无向图的一些信息:
- 要想知道某个顶点的度,只需要查该顶点的边表中结点的个数。
- 要判断顶点 vi 到 vj 是否存在边,只需要判断顶点 vi 的边表中 adjvex 是否存在 vj 的下标 j。
- 要查看顶点的所有邻接点,只需要对该顶点的边表进行遍历即可。
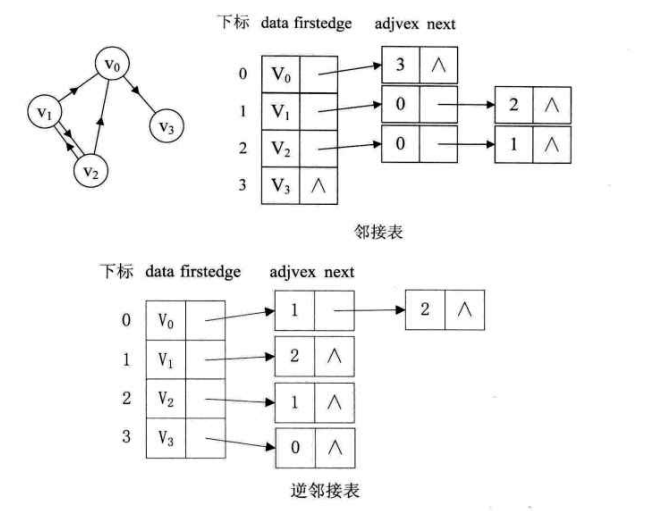
# 有向图表示
有向图的邻接表结构和无向图类似,但是由于有向图有方向,所以一般以顶点弧尾来存储边表,如下图中的第二幅图所示。如果要使用弧头来存储边表,可以参考下图中的第三幅图,这蔗农这种存储方式称作有向图的逆邻接表。
# 带权图表示
对于带权图,可以在边表的结点定义中增加一个 weight 域,用来存储权信息。
# 十字链表
邻接表对于无向图来说是非常不错的选择,但是对于有向图还是有一些局限。邻接表关心了有向图的出度问题,要想了解入度就需要遍历整个图;如果采用逆邻接表的话,解决了入度的问题,但是解决不了出度的问题,而十字链表刚好可以解决这个问题。
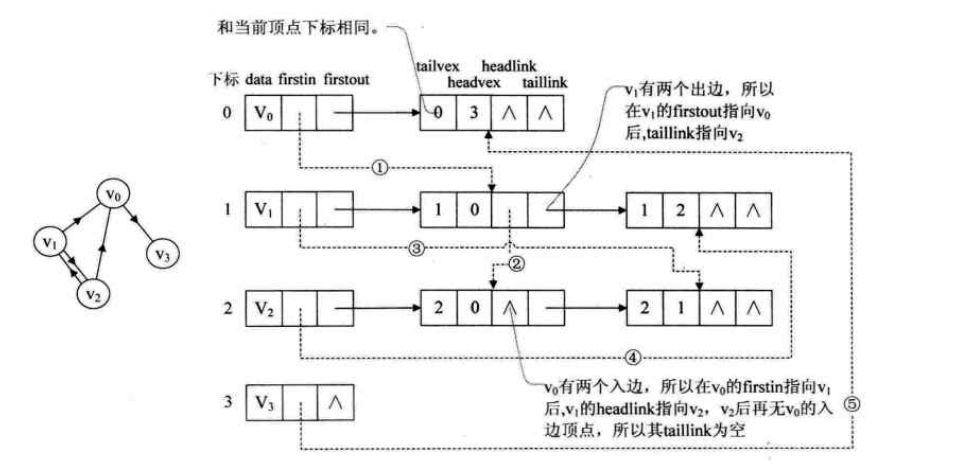
十字链表中顶点表结点结构如下所示。data 表示数据域,firstin 表示入边表头指针,指向该顶点的入边表中的第一个结点,firstout 表示出边表头指针,指向该顶点的出边表中第一个结点。

十字链表中边表结点结构如下所示。tailvex 是指弧起点在顶点表的下标,headvex 是指弧终点在顶点表中的下标,headlink 是指入边表指针域,指向终点相同的下一条边,taillink 是指出边表指针域,指向起点相同的下一条边。如果是网,还可以再增加一个 weight 域来存储权值。

对于下图图左的有向图,其十字链表示法如右图所示。右图边表中的 tailvex 和 headvex 实际上可以看做是边 <tailvex,headvex>,如顶点 V0 的第一个出边是边 <V0,V3>,所以 V0 的的 firstout 指向边表中的 <V0,V3>。由于 tailvex 是指弧起点在顶点表的下标,所以每个顶点实线指向的边表中的 tailvex 和顶点的下标是相同的;由于 headvex 是指弧终点在顶点表中的下标,所以每个顶点的虚线指向变表中的 headvex 和顶点的下标也是相同的。图中的实线实际上代表的是邻接表,而虚线表示的是逆邻接表,十字链表的好处就是将邻接表和逆邻接表结合到一起了。
# 邻接多重表
十字链表是对有向图的优化存储结构,而邻接多重表则是对无向图的优化存储。对于重点关注顶点的图来讲,邻接表是一种不错的选择,但是针对重点关注边操作的图来说,邻接表并不是那么友好。如下图所表示的邻接表,如果要删除边 (v0,v2),则需要同时删除 v0 的边表中的第 2 个结点和 v2 的边表中的第一个结点。

由于邻接表对边操作频繁的情况并不是特别友好,所以才出现了邻接多重表。邻接多重表中边表结点的结构如下图所示:

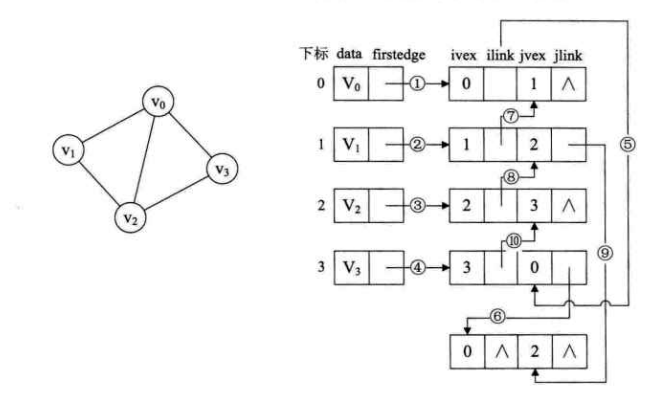
其中 ivex 和 jvex 是与某条边依附的两个顶点在顶点表中的下标。ilink 指向依附顶点 ivex 的下一条边,jlink 指向依附顶点 jvex 的下一条边。这就是多重表结构。
下图左图是一个有 4 个顶点 5 条边的无向图,右图用多重表的结构定义了顶点和边的数据结构。
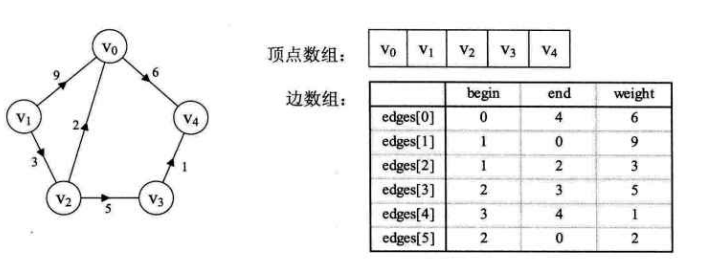
# 边集数组
边集数组是由两个一维数组构成。一个存储顶点的信息,另一个存储边的信息,这个边数组每个元素由一条边的起点下标(begin)、终点下标(end)和权(weight)组成。边集数组更适合对边依次进行处理的操作,而不适合对顶点的操作。